コンテンツ
待望の新コインボス登場!
来る7月11日、新たなコインボスの実装が決定しました!
その新ボスとは、なんと驚愕の・・・!

帝国三将軍!


まあコインボス自体は的中率99.9%の賭けにもならない予想通りだったわけですが、それと同時に色々と物議を醸しそうな「燃料」がぶっ込まれてきました。

問題のキャンペーンとは!?

『おでかけ超便利ツール』帝国三将軍リリース記念5大キャンペーン!
三将軍コイン実装の告知と同時に掲載されたのがコレ。
7月11日のメンテ後から1週間、「お得に」新コインを入手できるキャンペーンだそうです。

具体的なキャンペーン内容
(便利ツールで)オーグリード100連ふくびきが1回無料


(便利ツールで)オーグリードふくびきの1等~3等確率が2倍

(便利ツールで)オーグリード100連/1000連ふくびきの消費ジェムが割引


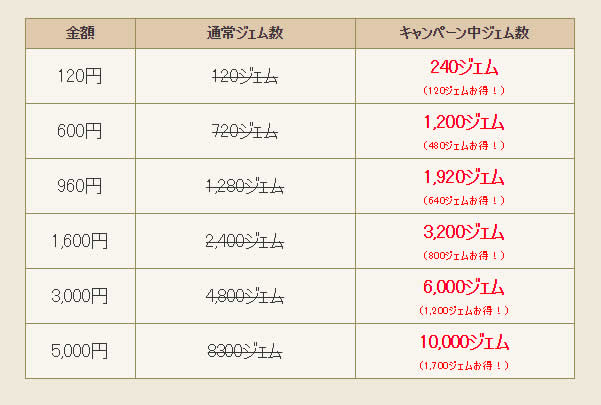
便利ツールの課金ジェムのボーナス増量

キャンペーン中に便利ツールにログインで200ジェムプレゼント


何が問題なのか?
いや、まんまソシャゲのやり方ですよね、これって。
「初回○○連ガチャ無料!」とか、CMでもWeb広告でもよく見る謳い文句ですし。
百歩譲って好意的に捉えるとすれば、マイタウンメダル実装でふくびきの需要が大きく「ツールふくびき」に偏り、オーグリードのふくびきが回されずに新コインの流通が滞る可能性があるため、それに対するテコ入れと考えることもできるかもしれません。
ただ、それだったらゲーム内でやれよ、って話だと思います。
ゲーム内において「オーグリードふくびきの上位当選確率を上げます」だけで十分効果があるでしょう。

そう考えると11日実装ってのもどうかと思ってしまいます。
テンの日にカードをサプライズ配布してもよかったんじゃないかと。
1枚で目的が達せられるものではないんですから、それが呼び水になって「もっとコイン買おう、もっとオーグリードで回そう」と経済が回る可能性も高いと思います。
今後の方向性への不安
Twitterやブログ等、他の方々の反応を見ていると、キャンペーン自体がお得か否かという評価は別として、「なんかおかしな方向に行ってないか?」という、今後の方向性への不安を感じている方が多いように感じました。
今後も新コインボスが実装される度に同じようなキャンペーンをやるのか?と考えると、何かそれは違うような気がします。
以前、FFのアプリを紹介した記事でも述べたのですが、わたしはガチャを始めとする「ソシャゲ」の要素をあまり好ましく思っていません。
運営は長らく「ふくびきはガチャではない」という主張をしていましたが、それはAppleには通用しなかったわけですよね。(結局、当選確率を明示するようになった)
そこで一度便利ツールの立ち位置などを再検討するべきだったのですが、むしろそれからは「ガチャとして認められてしまった以上、今後は開き直ってガンガン課金誘導していくぜ」といった方向に突き進んでしまったように思います。
今回のキャンペーンはそこが露骨に表れていますよね。
個人的には9日のDQXTVで今回のキャンペーンについて何かしらの見解を示してもらえればな、とは期待しています。
ということで、自分の中に湧いた違和感について書かせていただきました。
よろしければ、アンケートへのご回答とブログランキングの応援をお願いいたします!!


























さっさと引退したら?君も楽になるよ
終わりの始まり・・
今回のジェム回収、振り返ると『あぁ、あの時から・・』とかにならなければいいんだけどねー。
本当にそう思います。
どうしても違和感や不安がぬぐえません。